Kongruenzabbildungen im zweidimensionalen Raum

Beispiele für Kongruenzabbildungen

 

Wiederholung

Kongruenzabbildung ordnen jedem Punkt P(x|y)  der zweidimensionalen Ebene R2  in eindeutiger Weise einen Bildpunkt P‘(x‘|y‘)  aus R2 zu. Der Zusammenhang zwischen den Koordinaten der Punkte P  und P‘  kann durch 2×2-Matrizen und Vektoren beschrieben werden.
Die bereits aus der Sekundarstufe I bekannten Kongruenzabbildungen Spiegelung, Drehung und Verschiebung können durch Abbildungsgleichungen bzw. mit Hilfe von Matrizen und Vektoren dargestellt werden.

Spiegelung an der x-Achse

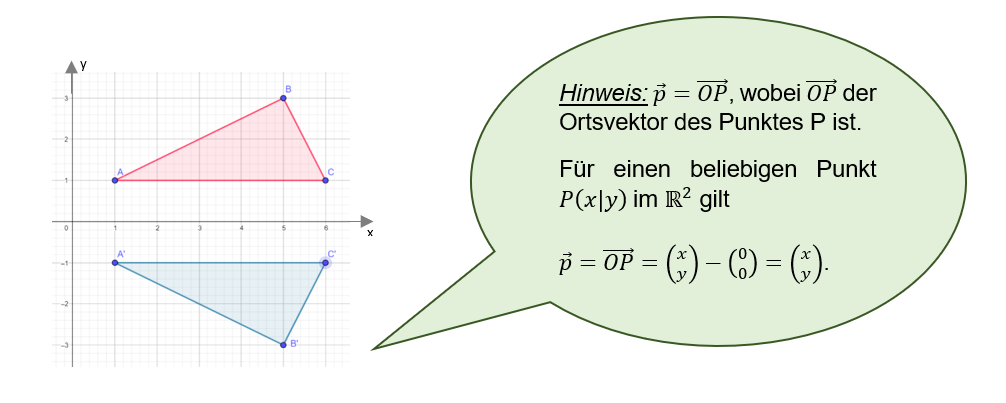
Ermittle die Koordinaten der Bildpunkte von A, B  und C.

Der Punkt A(1,1) wird gespiegelt auf den Bildpunkt A'(___,___)
  B(5,3)   B'(___,___)
  C(6,1)   C'(___,___)

 

Dieser Zusammenhang kann auch durch die linksseitige Multiplikation des Ortsvektors des Punktes P  mit einer quadratischen 2×2-Matrix A (Abbildungsmatrix) beschrieben werden.

Wie lautet die Abbildungsmatrix bei der Spiegelung an der x-Achse?

MERKE:

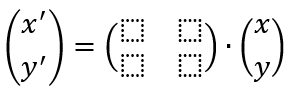
Bei der Spiegelung an der x-Achse wird der Punkt P(x|y)  auf den Punkt P‘ (    |    )  abgebildet.

Die Koordinaten x‘  und y‘  des Bildpunktes P‘  ergeben sich daher nachfolgenden Abbildungsgleichungen x‘=  _____, y‘= _____.

 

Translation (Verschiebung)

 

MERKE

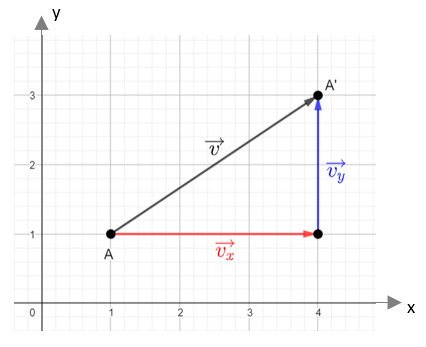
Bei der Translation (Verschiebung) um vx  in x-Richtung und vy  in y-Richtung, wird der Punkt P(x,y)  auf den Bildpunkt P' (_________ ,__________)  abgebildet.

Eine Translation kann mit Hilfe des Verschiebungsvektors v wie folgt beschrieben werden: p'=p+v .

 

Ermittle die Koordinaten der Bildpunkte von A, B  und C  bei der Verschiebung um den Vektor (-3,8).

Der Punkt A(-2,5) wird abgebildet auf den Bildpunkt A'(___,___)
  B(1,17)   B'(___,___)
  C(12,-2)   C'(___,___)

Definition der affinen Abbildungen

Viele der uns bisher bekannten Abbildungen lassen sich mit Hilfe einer Abbildungsgleichung der Form p'=A∙p  mit der 2x2-(Abbildungs-)Matrix A beschreiben. In diesen Fällen spricht man von linearen Abbildungen.
Die oben beschriebene Translation (Verschiebung) mit der Abbildungsgleichung  p'=p+v  passt nicht in dieses Schema und ist dementsprechend keine lineare Abbildung. Dennoch kann auch bei Verschiebungen eine Matrix mit ins Spiel gebracht werden:

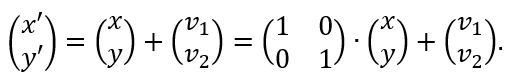
Die Matrix A wird in diesem Fall auch als 2x2-Einheitsmatrix E bezeichnet.

MERKE

Auf diese Weise können also nun alle bisher betrachteten Abbildungen durch eine Gleichung der Form p'=A∙p+v  beschrieben werden. Sie werden als affine Abbildungen bezeichnet und setzen sich aus einer linearen Abbildung A∙p  und einer Translation um den Vektor v  zusammen (affins [lat.]: verwandt, verschwägert).

Hinweis:
Bei den linearen Abbildungen ist der Verschiebungsvektor v  der Nullvektor. Somit stellen lineare Abbildungen einen Spezialfall der affinen Abbildungen dar.